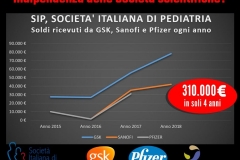
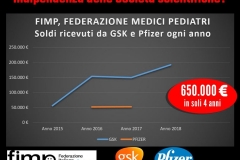
Marcello Pamio

Il suo vero nome era Leonardo Pisano ma il mondo lo conosce come Fibonacci.
Leonardo è nato a Pisa nel 1175 ed è morto nella stessa città nel 1235 circa. Figlio di Guglielmo dei Bonacci, un rappresentante di mercanti della repubblica marinara di Pisa da cui deriva il nome Fibonacci, e cioè “Filius Bonacci”.
Senza ombra di dubbio è uno dei più grandi matematici del mondo che riuscì a fondere assieme la geometria greca euclidea con la matematica elaborata dalla scienza araba e da quella alessandrina.
L’Italia stava vivendo un periodo molto intenso dal punto di vista culturale, artistico e scientifico grazie ai traffici con l’Oriente delle repubbliche marinare.
Leonardo assieme al padre passò molti anni in Algeria dove poté studiare l’aritmetica degli arabi musulmani e la geometria euclidea.
Crebbe a Bugia ad Algeri dove il padre era impiegato di dogana per conto di alcuni mercanti pisani, e lì venne stato istruito con l’abaco (una specie di pallottoliere) ad usare la numerazione arabica del tutto ignorata fino a quel momento in Europa. Fu qui infatti che apprese il sistema numerico indo-arabico, che corrisponde all’attuale sistema decimale fondato sulle dieci cifre da 0 a 9. Sistema molto più pratico per effettuare i conti rispetto al classico romano, soprattutto per la presenza dello “0” ad indicare l’assenza di qualcosa. Per noi cosa scontata, ma non per l’epoca e soprattutto era di enorme aiuto nell’effettuare i calcoli (per i commercianti)!
Viaggiò moltissimo nel Nord Africa ed in tutto il Mediterraneo conoscendo i più grandi scienziati e intellettuali arabi del tempo.
Le sue incredibili abilità e capacità nel risolvere problemi di matematica arrivarono fino alle orecchie dell’imperatore Federico II di Svevia, regnante in Sicilia dove, tra il 1230 e il 1250 fondò la famosissima e prestigiosa Scuola Siciliana, centro culturale unico del Mediterraneo.
Federico II consegnò a Leonardo un assegno che gli permise di dedicarsi completamente ai suoi studi matematici.
Tra le sue opere, la più importante fu rappresentata da quattro libri: Liber Abaci, LiberQuadratorum, PracticaGeometriae e Flos.

Successione o serie di Fibonacci
Cercando di trovare una legge matematica che descrivesse la crescita di una popolazione di conigli, Leonardo arrivò alla scoperta della successione che prese il suo nome, composta da numeri dove ogni elemento è dato dalla somma dei due che lo precedono. 1, 1, 2, 3, 5, 8, 13, 21…
Questa sequenza in realtà era già nota ai matematici arabi e anche a quelli indù fin dai tempi antichi.
Il nome “numeri di Fibonacci” fu dato nel diciannovesimo secolo dal matematico francese Edouard Lucas (1842-1891), celebre anche per il gioco della “Torre di Hanoi”.
La magia sta nel fatto che il rapporto tra questi due numeri successivi si avvicina molto rapidamente a 0,618 (1:2= 0,5; 2:3= 0,667; 3:5= 0,6; 5:8= 0,625; 8:13= 0,615; 13:21= 0,619…).
Quindi il rapporto tende a 1,618, il famoso “Rapporto aureo” chiamato anche la “proporzione divina”, un numero irrazionale che ha misteriose proprietà…
Attorno all’anno 1228, cioè verso i cinquant’anni Fibonacci scomparve completamente dalla scena…
Abbiamo detto che i rapporti tra due numeri affiancati della successione danno come risultato la costante Phi della sezione aurea (ϕ=1,618033…).
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144, 233, 377, 610, 987,1597, 2584, 4181, 6765,10946, 17711, 28657, 46368, 75025
Il numero aureo è una costante matematica indicata con la lettera greca φ, ed è per definizione il rapporto tra due grandezze in proporzione aurea.
Il numero aureo vale ((1+√5)/2):
ϕ=1,6180339887…
Sezione Aurea
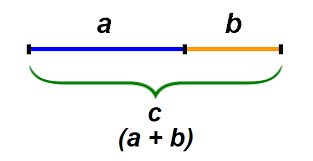
Un altro modo per definire la Sezione Aurea è prendere un numero A e un numero B e dire che A+B sta ad A come A sta a B.
Quindi φ→(A+B) : A = A : B
Il segmento totale C (A+B) sta al segmento più lungo A, come A sta al segmento più corto B:
C : A = A : B = φ
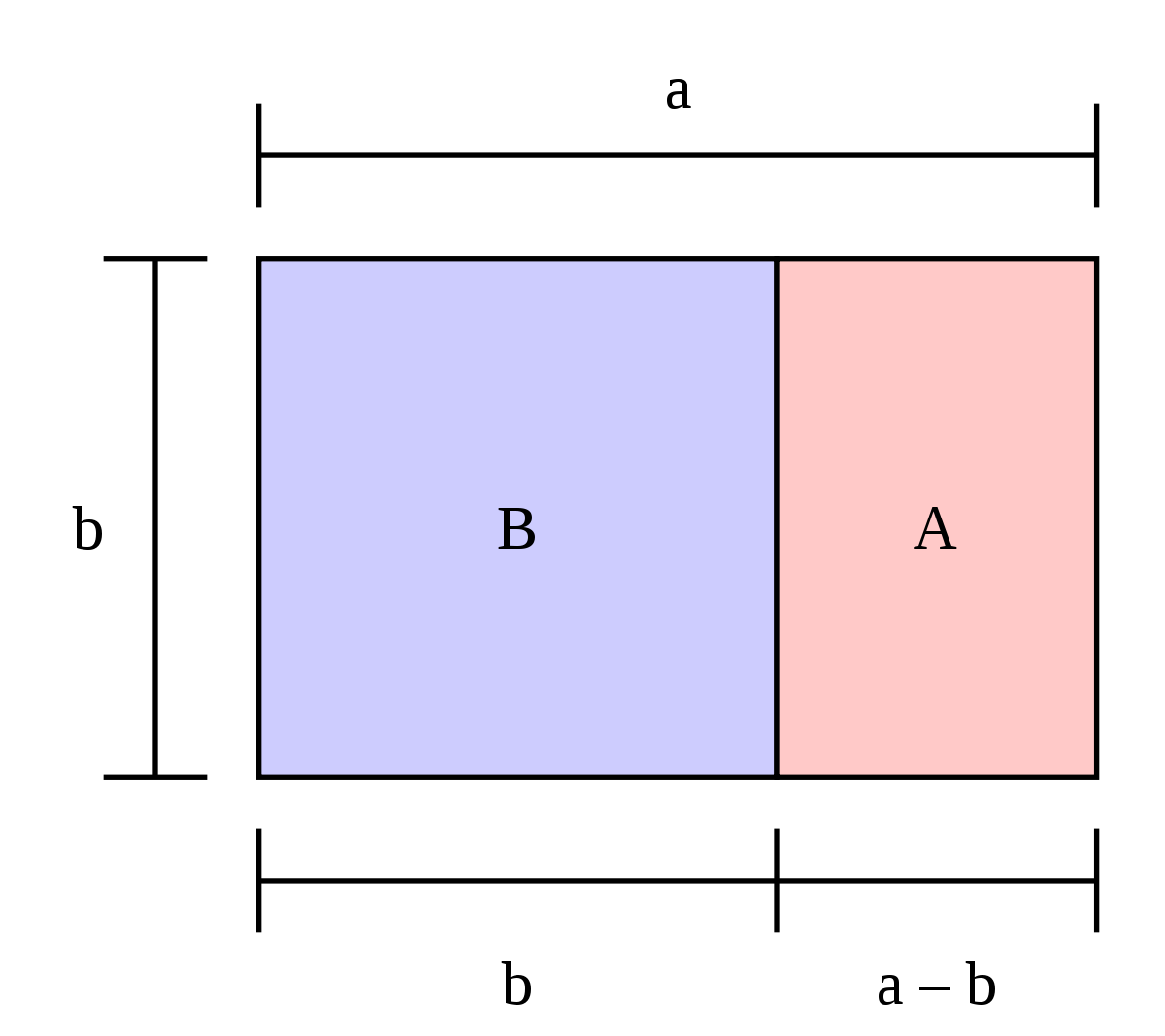
Rettangolo aureo
Un rettangolo è aureo quando le sue dimensioni soddisfano la proporzione aurea!
I due lati del rettangolo stanno tra loro nel rapporto definito dalla Sezione Aurea.
Volendo esprimere in formula la definizione di rettangolo aureo, il lato maggiore è A e quello minore è B.
A : B = B : (A-B)
Dal rettangolo aureo si può partire e disegnare la famosissima Spirale Aurea o di Fibonacci.
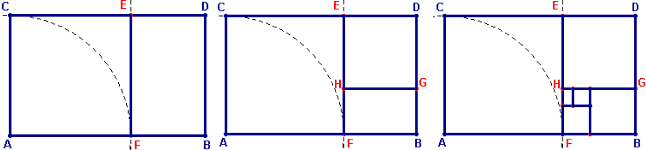
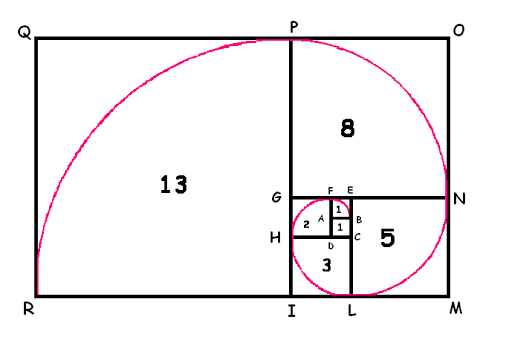
Proporzioni che danno vita alla forma estetica perfetta!
Dagli Egizi a Leonardo Da Vinci arrivando ovviamente fino al matematico Fibonacci tutti hanno ampiamente usato questa proporzione considerata Divina.
Troviamo la spirale aurea nelle micro-SIM telefoniche, nella facciata del Partenone di Atene, nella Gioconda di Leonardo, nella piramide di Cheope, nella struttura delle conchiglie, nella disposizione dei petali dei fiori, nei cicloni, ecc.